アナログなデータ
時間軸に対して連続的なデータを持つもの。例えば、声やレコード、アナログ放送などがある。
ここで中学生のころ習ったであろう式や図が重要になってくる。
式: f(t) = sinx(t)
※変数tは、少数を含む整数。(→データが飛び値でない)
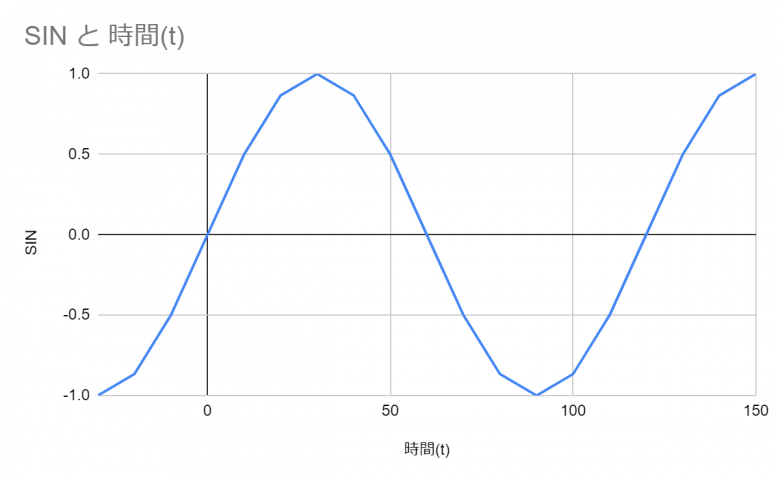
こういった連続的なデータがアナログといえる。
ディジタルなデータ
時間軸に対して離散的なデータを持つもの。例えば、CDやDVD、ディジタル放送などがある。
ここでもアナログ同様式と図を示そう。
式: f(t) = sinx(t)
※変数tは、整数(少数は含まない)。(→データが飛び値である)

アナログからデジタルデータへ変換
まずは以下2つの図をご覧いただきたい。最初の図はこれまでに出てきたアナログのデータだ。次の図はこの波をディジタルに変換した波になる。要するにアナログの山を値”1″に、谷を値”0″に一つ一つ変換していることを表している。雑に言うとアナログとディジタルの関係はそんなものだろう。

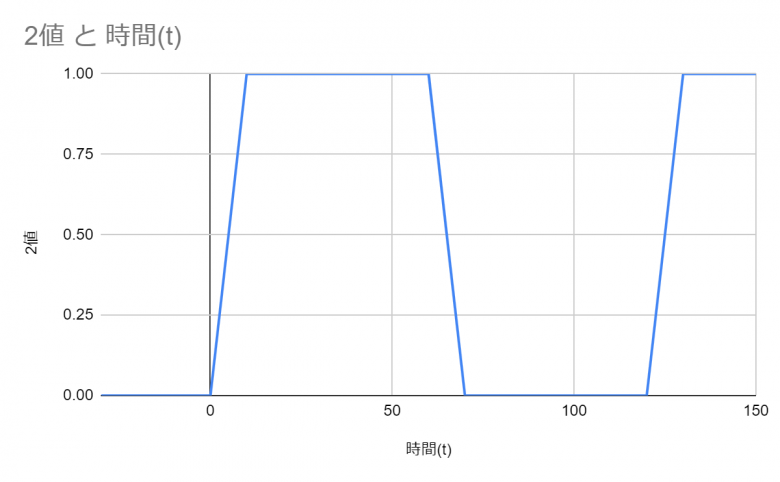
ただこれだけでは後で自分で見返しても「??? だからなに?」と思ってしまうのでより具体的に考えていこう。
以下の図の波を声(アナログ)として扱おう。で、これを録音してディジタルなデータに変換しパソコンに保存することを想定する。

これを先ほどと同様にディジタルに変換する、のはやめておこう。ディジタルは2値しかとらない。普通音声通話で2音しか聞こえてこないような、モールス信号のような形で通話している人はいないだろう。
ではどのようにしてアナログからディジタルなデータに変換するかというと、上の図から標本化・量子化を経てディジタルに変換する。
まずは標本化だ。標本化では一定の周期の値のみ抽出する。今回上の図から周期30で値をとると以下のような図になります。(本当は線ではなく点で表現したかったのですが、工数かけたくなかったのでご勘弁。)上の図では周期30ごとに谷→中央→山と変化してくデータで作成しているため、標本化すると周期30で-1→0→+1の値をとるようになっている。
つまり、この周期を調整することで時間軸に対するデータの粒度が決定する。周期を短くするほど標本化するデータ量が多くなり、実際の声(アナログ)のデータに近くなる。もう少しわかりやすく言うと周期を短くするとパラパラ漫画がよりアニメーションっぽくなるし、周期を長くするほどカクついた動画になるイメージ。
(今回は図を作るのが面倒なので-1, 0, +1のデータしかとらないけど許して…。)

さらにここから量子化を行う。量子化はデータの精度をどの程度担保するかを決定する、といったところか。コンピュータに記録されるデータは値”1″か”0″を記録するマスの塊なのだ。例えば数値”1″は1bit(21)で、数値”32″は5bit(25)で、数値”256″は8bit(28)で表現できる。ここで、音のデータとして考えていただきたいのだが、1音しか表現できないデータと32音表現できるデータ、256音表現できるデータしか選べないとして、あなたはどれで音楽を聴きたいですか?もちろん256音の方ですよね。と、いうのが制度をどの程度担保するかを決めるということなのだ。
まぁ改めてなんだけど、周期は単位時間当たりのデータ量を表し、周期が短いほどデータ量が多くなるため時間軸に対する精度が高まる。量子化ではデータ軸方向に対する精度を高めることができ、そのためにはビット数を増やして表現できるデータの幅を増やす。
結論
アナログとディジタルの違いは…。
アナログ…生データ。観測したデータ。省略できない(概念がない)。データ量が多い。
ディジタル…サンプリングデータ。精度調整可能。比較的データ量は少ない。
若者よ。勉強しよう!今のうちに。俺のようにならないように…。
文字にすることや書くのが面倒で適当で読みにくいでしょうが、ごめんなさい。
ピンバック: アナログとディジタルの電波の解釈 – E-Lab / Engineer Laboratory